Lab #2 Classical Statistics Experiment

Conceptual goal: Apply a statistical analysis to a classical system.
Computational goal: Learn and use basic Matlab: making tables, plotting, curve fitting, publishing.
Experimental goal: Use a Boltzmann machine to determine the fraction of time a ping-pong ball spends on the upper level of a two-level system.
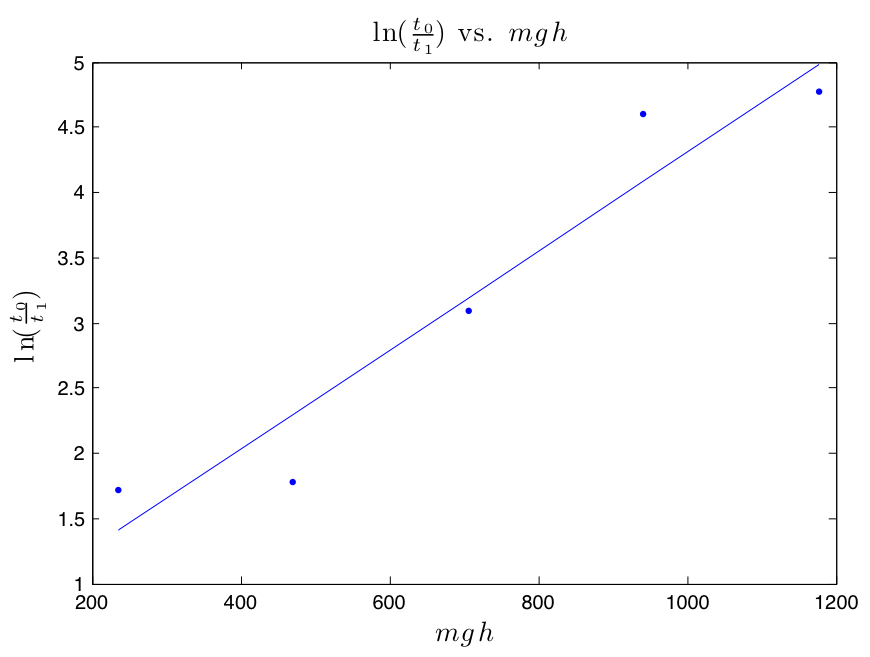
When students are first exposed to quantum mechanics they face several difficulties. First, as suggested by L. Bao and E. F. Redish [1], it is traditionally assumed that students understand probability and energy level diagrams, yet they cannot relate a probabilistic representation to an actual observation. In this laboratory, students will use a Boltzmann machine, as suggested by J.J. Prentis [2] to simulate canonical statistics. The Boltzmann machine consists of a two-level system with a motorized ball confined to each level, and a ping-pong ball that is free to move between levels. The time that the ping-pong ball spends in each level is an exponential function of the energy gap of the system (mgh, where m is the mass of the ping-pong ball, g is the gravitational constant, and h is the height difference of the two levels). The concept of degeneracy of a level is introduced, as it is proportional to the surface area of each level. If a0 is the area of the lower level and a1 the area of the upper level, then the ratio of the time the ping-pong ball spends at each level is simply
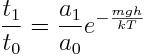
where the temperature factor, kT, corresponds to the average kinetic energy of the ping-pong ball.
Students are asked to make a prediction for the ratio of the time the ping pong ball spends on the upper and lower levels of the Boltzmann machine. They then observe patterns on the Boltzmann machine, and modify their predictions in order to explain the experimental results.
2. J. J. Prentis, “Experiments in statistical mechanics,” Am. J. Phys. 68, 12 (2000).
Computational goal: Learn and use basic Matlab: making tables, plotting, curve fitting, publishing.
Experimental goal: Use a Boltzmann machine to determine the fraction of time a ping-pong ball spends on the upper level of a two-level system.
When students are first exposed to quantum mechanics they face several difficulties. First, as suggested by L. Bao and E. F. Redish [1], it is traditionally assumed that students understand probability and energy level diagrams, yet they cannot relate a probabilistic representation to an actual observation. In this laboratory, students will use a Boltzmann machine, as suggested by J.J. Prentis [2] to simulate canonical statistics. The Boltzmann machine consists of a two-level system with a motorized ball confined to each level, and a ping-pong ball that is free to move between levels. The time that the ping-pong ball spends in each level is an exponential function of the energy gap of the system (mgh, where m is the mass of the ping-pong ball, g is the gravitational constant, and h is the height difference of the two levels). The concept of degeneracy of a level is introduced, as it is proportional to the surface area of each level. If a0 is the area of the lower level and a1 the area of the upper level, then the ratio of the time the ping-pong ball spends at each level is simply
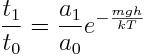
where the temperature factor, kT, corresponds to the average kinetic energy of the ping-pong ball.
Students are asked to make a prediction for the ratio of the time the ping pong ball spends on the upper and lower levels of the Boltzmann machine. They then observe patterns on the Boltzmann machine, and modify their predictions in order to explain the experimental results.
References:
1. L. Bao and E. F. Redish, “Understanding probabilistic interpretations of physical systems: A prerequisite to learning quantum physics,” Am. J. Phys. 70, 3 (2002).2. J. J. Prentis, “Experiments in statistical mechanics,” Am. J. Phys. 68, 12 (2000).
