Lab #3 Classical Statistics Simulation
A classical particle in a two-dimensional box with a step
Conceptual goal: Develop familiarity in applying statistics to classical physics.
Modeling goal: Gain an understanding of what is an appropriate time-step and how long to run a model. Develop an awareness of the interplay between theory, modeling and experiment.
Computational goal: Nested for loops, animations.
The computational component of this laboratory consists of modeling the Boltzmann machine used in the previous laboratory. The ping-pong ball's collisions with the squiggle balls are simulated as random changes in the velocity of the particle. We guide the students through the modeling process, but leave enough room to allow for students to make decisions about important physical aspects such as initial conditions, what data to record, and how to analyze the data. Similarly to the experiment, the time the particle spends in the upper and lower levels are related by the Boltzmann factor:
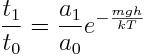
References:
1. L. Bao and E. F. Redish, “Understanding probabilistic interpretations of physical systems: A prerequisite to learning quantum physics,” Am. J. Phys. 70, 3 (2002).2. J. J. Prentis, “Experiments in statistical mechanics,” Am. J. Phys. 68, 12 (2000).
This material is based upon work supported by the National Science Foundation under Grant Number DUE-1140034.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
