Lab #9 Quantum Dots Particle-in-a-Box Model
Modeling goal: Learn how differential equations are discretized and solved in a computer.
Computational goal: Eigenvalues and eigenvectors in Matlab.
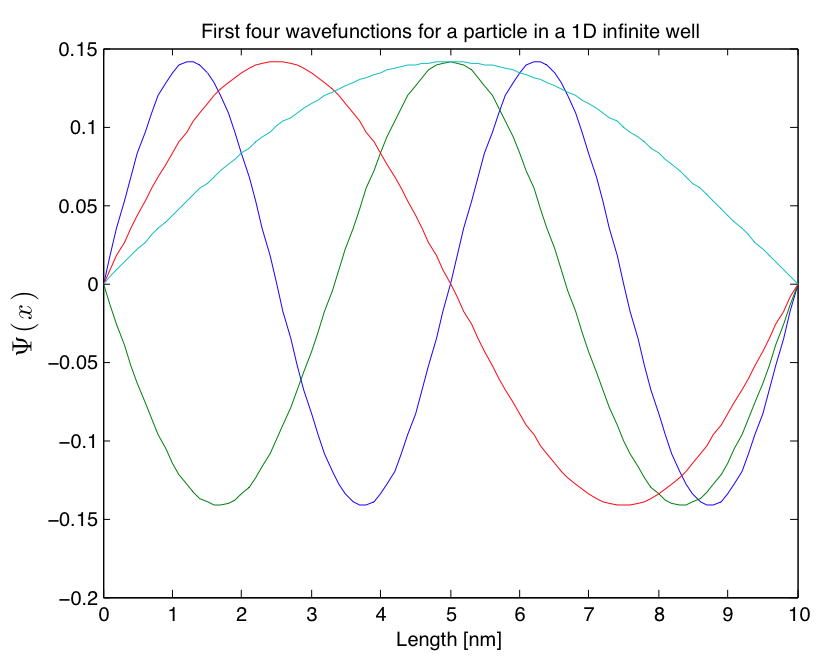
Students are asked to model Quantum Dots in Matlab by numerically solving for the first few eigenvalues and eigenfunctions of the three-dimensional Schrödinger equation for a particle in a box with infinite potential outside the box. Our students are generally enrolled in differential equations, but have not taken linear algebra by the time they take Applications of Modern Physics. We have developed a handout (adapted in part from references 1 and 2) where students are guided through how to discretize functions, use the finite difference approximation for the second-order derivative, write the Schrödinger equation as a Hamiltonian matrix, and finally diagonalize the matrix to obtain the eigenvalues and eigenfunctions.
References:
1. A. F. J. Levi, Applied Quantum Mechanics, 2nd ed. Cambridge University Press, United Kingdom (2006).2. W. Cheney and D. Kincaid, Numerical Mathematics and Computing, 5th ed. Thomson Brooks/Cole, United States of America (2004).
