
PHYS 341: Electricity and Magnetism
Instructor and Team Leader: Jeff Jalkio
The first half of a two-semester sequence, this junior/senior level course covers electro- and magneto-statics and Maxwell’s equations, while the second semester covers wave propagation and applications such as antennas and transmission lines. This course does not have a lab component, and many students find the abstract material difficult to grasp. Since the course deals with fields that are invisible and remote from daily experience, the material is typically presented mathematically, and analytical methods are used to solve problems. However, only the simplest of cases can be solved analytically, and most real-world applications of electromagnetics use finite element methods to find numerical solutions. We believe that the use of experimental and computational elements in this course would improve student understanding of the material and provide them useful professional tools. Our goal in this class is to use MATLAB to perform calculations of electric potentials to introduce finite difference methods to the students. Coupled with in-class validation experiments, the calculations will help students visualize the meaning of the mathematical formalisms used throughout the semester.
In-class Exercise: Electric Potential of Two-dimensional Systems
Conceptual goals: Understand how finite difference methods can be used to solve Laplace’s equation to determine electric potentials. Visualize electric fields for non-trivial geometries, such as microstrip transmission lines.
Computational goals: Use conductive paper to map the electric potential for two-dimensional systems.
Experimental goal: Learn how to use finite difference methods in MATLAB.
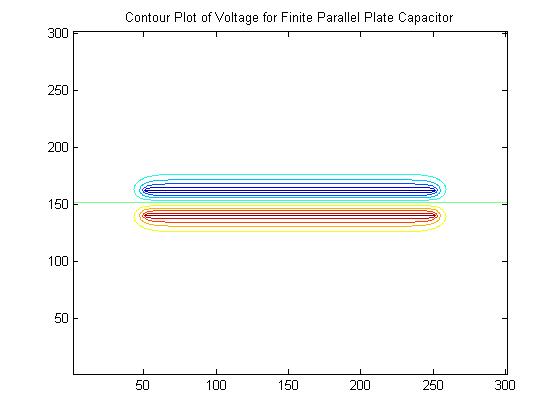
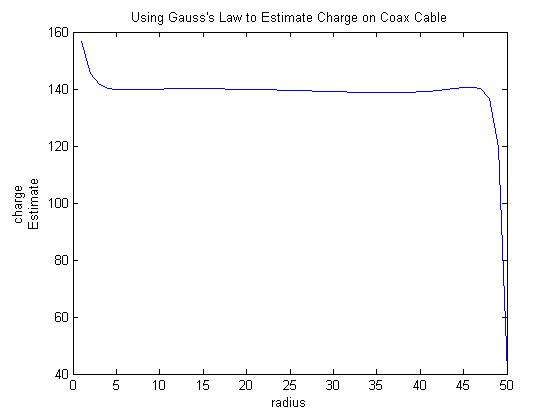
Prior to this unit, students will have learned to find the electric potential analytically for several simple geometries such as infinitely long concentric cylinders. However, these analytical approaches do not yield solutions for more complex geometries that lack symmetry. In this unit, students will see through in-class demonstrations that conductive paper can be used to map electric potentials and that these experimental results match analytical results calculated in class for a case where an analytical result is available (e.g., the electric field and potential in a coaxial cable). Although this method provides a way to measure potentials for more complex geometries, the approach is labor intensive and tedious. We will then introduce finite difference methods for solving Laplace’s equations. Currently, this method is discussed in class, but the students do not have the opportunity to use the technique in homework assignments. We will develop a MATLAB assignment in which students use finite difference methods to find a potential, which will allow them to test their understanding and gain practice in this useful skill. In the case of a coaxial cable, the calculation can be done in a one-dimensional or two-dimensional approach and the results can be compared to both experiment and theory for verification. Once students are comfortable with their ability to model two-dimensional problems, we will ask them to model a practical configuration like a microstrip transmission line that lacks the symmetry needed for analytical solution, but is commonly used in circuit boards. This geometry will also be modeled via conductive paper so that students can validate their simulation results with experimental data.
Sample Results:



The first half of a two-semester sequence, this junior/senior level course covers electro- and magneto-statics and Maxwell’s equations, while the second semester covers wave propagation and applications such as antennas and transmission lines. This course does not have a lab component, and many students find the abstract material difficult to grasp. Since the course deals with fields that are invisible and remote from daily experience, the material is typically presented mathematically, and analytical methods are used to solve problems. However, only the simplest of cases can be solved analytically, and most real-world applications of electromagnetics use finite element methods to find numerical solutions. We believe that the use of experimental and computational elements in this course would improve student understanding of the material and provide them useful professional tools. Our goal in this class is to use MATLAB to perform calculations of electric potentials to introduce finite difference methods to the students. Coupled with in-class validation experiments, the calculations will help students visualize the meaning of the mathematical formalisms used throughout the semester.
In-class Exercise: Electric Potential of Two-dimensional Systems
Conceptual goals: Understand how finite difference methods can be used to solve Laplace’s equation to determine electric potentials. Visualize electric fields for non-trivial geometries, such as microstrip transmission lines.
Computational goals: Use conductive paper to map the electric potential for two-dimensional systems.
Experimental goal: Learn how to use finite difference methods in MATLAB.
Prior to this unit, students will have learned to find the electric potential analytically for several simple geometries such as infinitely long concentric cylinders. However, these analytical approaches do not yield solutions for more complex geometries that lack symmetry. In this unit, students will see through in-class demonstrations that conductive paper can be used to map electric potentials and that these experimental results match analytical results calculated in class for a case where an analytical result is available (e.g., the electric field and potential in a coaxial cable). Although this method provides a way to measure potentials for more complex geometries, the approach is labor intensive and tedious. We will then introduce finite difference methods for solving Laplace’s equations. Currently, this method is discussed in class, but the students do not have the opportunity to use the technique in homework assignments. We will develop a MATLAB assignment in which students use finite difference methods to find a potential, which will allow them to test their understanding and gain practice in this useful skill. In the case of a coaxial cable, the calculation can be done in a one-dimensional or two-dimensional approach and the results can be compared to both experiment and theory for verification. Once students are comfortable with their ability to model two-dimensional problems, we will ask them to model a practical configuration like a microstrip transmission line that lacks the symmetry needed for analytical solution, but is commonly used in circuit boards. This geometry will also be modeled via conductive paper so that students can validate their simulation results with experimental data.
Sample Results:



If you are interested in using any of the materials found in this webpage in your own course, please contact us.
